初中数学相关知识点 数学初中全部重要知识点讲解

关注“中考数学当百荟”，感谢您的支持！

初中数学学习中一些常用语

中考数学当百荟

在数学学习中，经常遇到一些习惯性说法。这些说法沿用历史悠久流传甚广，因而成为数学学习中约定俗成的口头语言和书面语言。

一.书写格式用语

1.解与证明

解：本义是解答的意思，常用于解答题型，解答者答题书写的第一个字。有提醒意味（相当于演讲开始前清嗓子，试麦敲话筒），表示答题开始，“解”字以后的话都是解答者的观点和解释，文责自负。

证明：根据条件，利用所学公理、定理推导命题的过程。常用于证明题型，解答者答题书写的句首，表示论述开始，“证明”二字以后的话都是解答者的观点和论述。

2.原式

原式：原来的代数式的意思。常用于化简、求值类题目，若式子较长或较复杂，常用“原式”二字代替。解答者答题书写在“解”字后面，“原式”后面必跟“=”，因而格式上写成“解：原式=”的样式。用“原式”二字代替一长串由字母和运算符号等组成的象动车一样长式子，是一种合理合法的“偷懒”行为，免去你抄写原代数式之苦，也能省不少笔墨和纸张，也为环保出一份力。但在实际中学渣们常容易犯三类错误：其一，已经够省了，还想再偷懒，写为“解=”；其二，解方程（不等式）类型的题目，是不用这种格式的；其三，将“式”字写残废了，经典的错误“工+戈”（常写残废还有另一个字“或”，后话，先按下不表）。

3.因为与所以

因为所以，常用在证明题型。连在一起组成“因为。。。，所以。。。”的样式，表示根据条件，推导结论的过程。实际中，因为所以也常用专用符号“∵∴”代替，但点阵的倒正学渣们易混。特别说明的是，虽然“∵∴”成对出现，但可以一个“∵”跟多个“∴”，这种情况往往是因为前一个“∴”又是下一步推理的条件，所以“∵”就省了（这段话有点绕，还是举例吧）。比如：∵1+2=3，5－2=3，∴1+2=5－2，∴1＋2＋2=5，∴1＋4=5.

二.数学概念用语

4.距离与绝对值

简单说绝对值就是距离，它表示两个数在数轴上相距多远。比如：3的绝对值，就表示3与0的距离；3－4的绝对值，就表示3与4的距离；那3＋4的绝对值呢？显然表示3与－4相距多远呗！反过来，求任意两个数a，b相距多远如何表示？就表示为|a－b|.

准确理解绝对值这个概念，要从以下四个方面把握：读法、记法、几何含义、其值是多少。比如看到| x－1|这个记号，读作：x与1差的绝对值，表示数x与1的距离，其值有三种可能：

x－1，0，1－x；依次对应的条件：x＞1，x=1，x＜1.因为距离不可能为负数，所以去掉绝对值符号，必须保证“大”减“小”！

5.垂直与相交

垂直与相交，特殊与一般的关系。相同点：都表示两条直线不是平行线。垂直是相交的一种特殊状态，当且仅当两条直线相交且所成角为直角（90°），此时，称之为两条直线互相垂直。关键是书面表达普遍搞错！直线a，b互相垂直，正确写法：a⊥b，垂足为M，不正确的写法：a⊥b于点M，符号“⊥”读作“垂直于”后面还跟“于”字，造成重复！

6.或与且

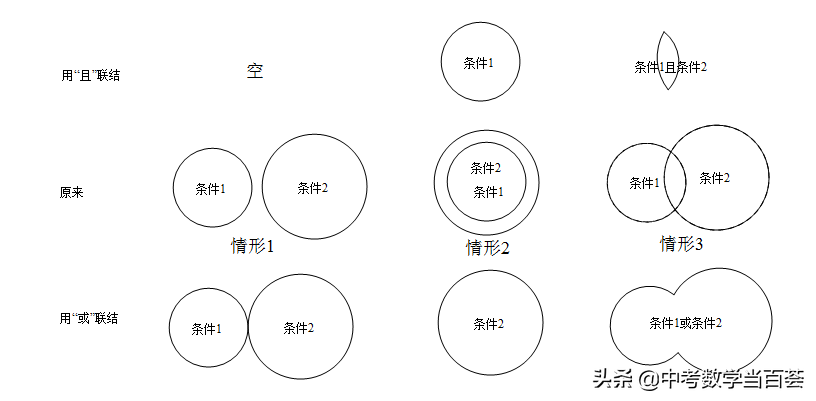
或与且，逻辑联结词。字面意思明了，区别明显。但在初中阶段想彻底理解，对大多数人来说，困难！高中学过集合运算、复合命题、排列组合等知识后，可能才会理解更深刻。对于初中生来说记住三点：其一，或，初学容易理解为非黑即白选择关系。多个条件用“或（or）”联结表示至少满足其一；其二，且，类似于语文连接词“既，又”，“不仅，而且”。多个条用“且（and）”联结，表示同时成立；其三，不要把“或”写残了，经典的错误 “戈”缺一撇。用图示意或与且的区别和联系吧！

7.根与解

解与根，表示解方程最后得到的正确结果，但常常让人傻傻分不清。想象一下，容器与容器中的东西。解是方程根的总称，类似于“容器”，而根类似于“容器中的东西”。具体来说，初中学段的两类整式方程：一元一次方程、一元二次方程。比如：方程x+1=0，其解唯一（x=-1），此时根就是解，解就是根；方程x^2-4x+3=0，有两个不相等的根（x=1，x=3），此时，方程的解就是3和4,而3或4只能称为方程的根，一字之差“和”与“或”，意思不同，仔细体会。类似于方程的“根”与“解”，还有不等式的“解”与“解集”。这些受学段内容限制，初中学段不学集合概念，没有建立集合元素与集合的概念，所以只能“容器”与“容器中的东西”来形象说明。

8.开平方与开方

开平方与开方，特殊与一般的关系。开方是初中学段所学六种基本运算中的一种，这六种基本运算分别是加、减、乘、除、乘方、开方。开方又包括开平方（开二次方）、开立方（开三次方）、开四次方。。。，而开平方、开立方，是开二次方、开三次方的简称，它们都只是开方运算的一种。

9.相等（=）与恒等（≡）

相等与恒等，简单说相等是有条件的，恒等是无条件的。比如：1+3=4，实际左右恒相等，此时1+3≡4，而x+1=0，左右相等是有条件的，除非x=-1，否则，左右不等。因而x+1=0，只是等式，不是恒等式;1+3=4,不仅是等式更是恒等式，还有乘法公式，如（a+b）（a-b）=a^2-b^2,(a+b)^2=a^2+b^2+2ab等都是恒等式。

10.两根内与两根外

两根内与两根外，求二次函数自变量取值范围时，一种常用的口语表达。因为初中学段不学一元二次不等式的解法，所以先求出函数值为0时，对应的自变量的值，即方程的两根，然后通过图象观察写出自变量取值范围是两根内还是两根外。比如：方程的两根是x1，x2，两根内即为x1<x<x2，两根外即为xx2.

关注“中考数学当百荟”，感谢您的支持！

关注“中考数学当百荟”，感谢您的支持！点击“了解更多”