线性代数的秘密：什么是线性？

什么是线性？话不多说，让我们开门见山：

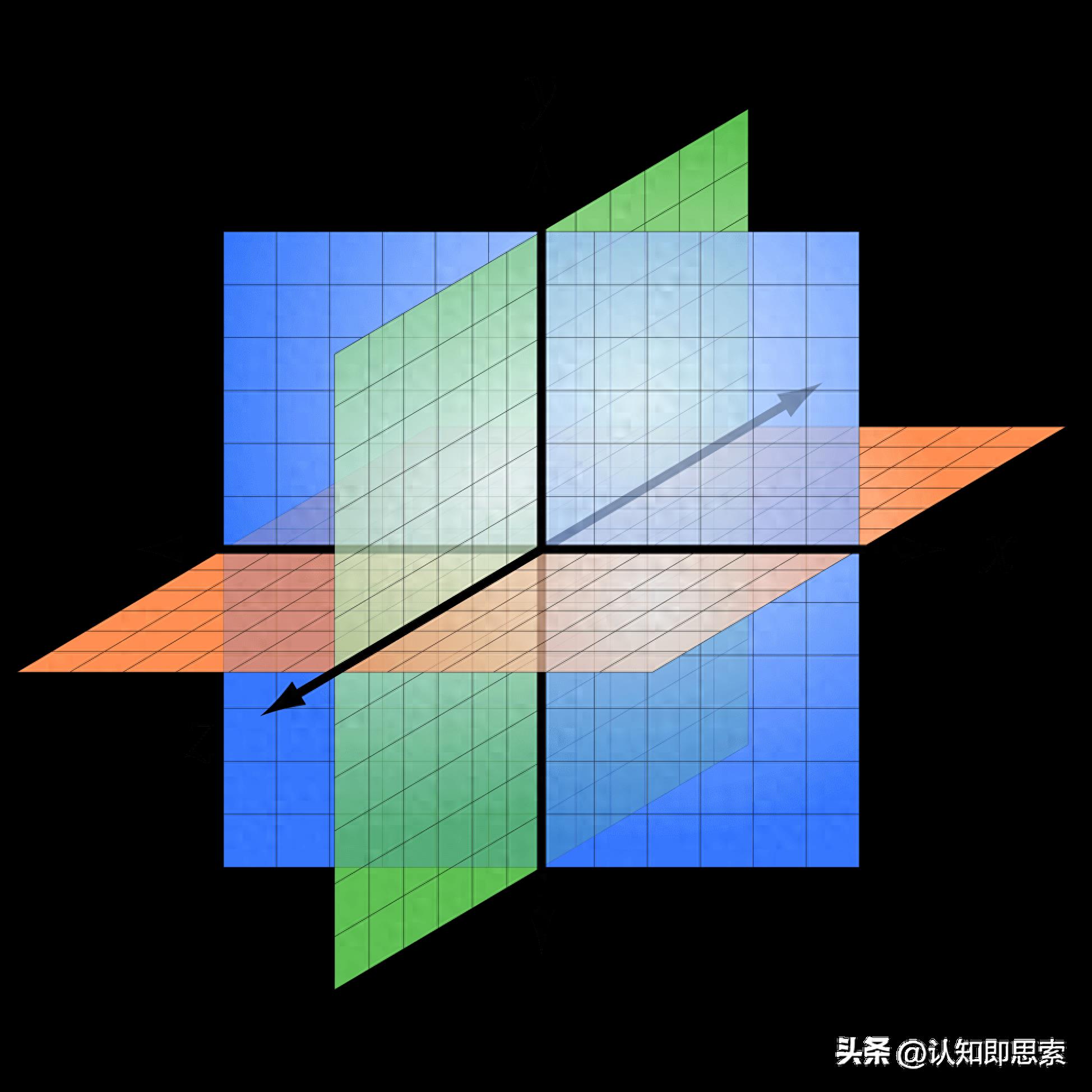
线性系统或函数具有以下特点：

可加性：当有两个输入值时，其输出值是这两个输入值的和。

齐次性：当所有输入值都乘以同一个非零常数时，输出值也将乘以该常数。

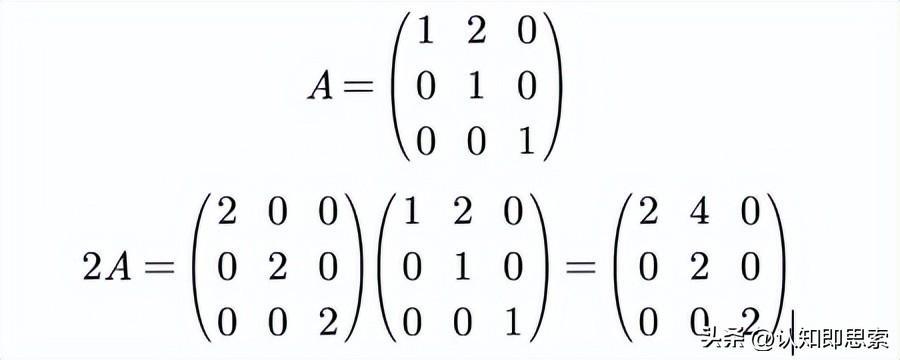
一次性：表达式中涉及的量（如标量、矢量、函数、矩阵、导数）的次数最高只能是一次，且没有这些量的乘法、除法、指数和对数运算。

线性空间：

那么“非线性代数”是什么？

非线性系统或函数则不满足以上特点，具有更复杂的性质。例如，系统的要素可能互相作用，或者具有特殊的关系。非线性系统或函数通常更难以理解和分析，但它们在自然界中普遍存在，并且能够产生丰富多样的行为和现象。

弯曲空间：

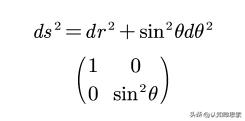
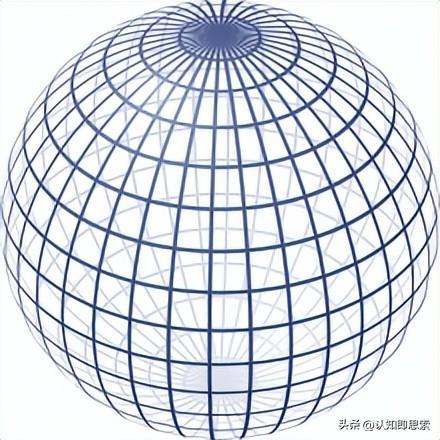
需要注意的是，线性和非线性并不是绝对的对立概念，而是描述系统或函数性质的相对方式。许多实际问题中，系统或函数既包含线性成分又包含非线性成分，需要综合考虑两者的影响。非线性代数是数学科学的一个新的门类和学科体系，它用来分析和解决混沌、分形等复杂问题。这个领域的核心是在元素分类、集合分解基础上的非线性群、非线性环、非线性域等方面的研究:

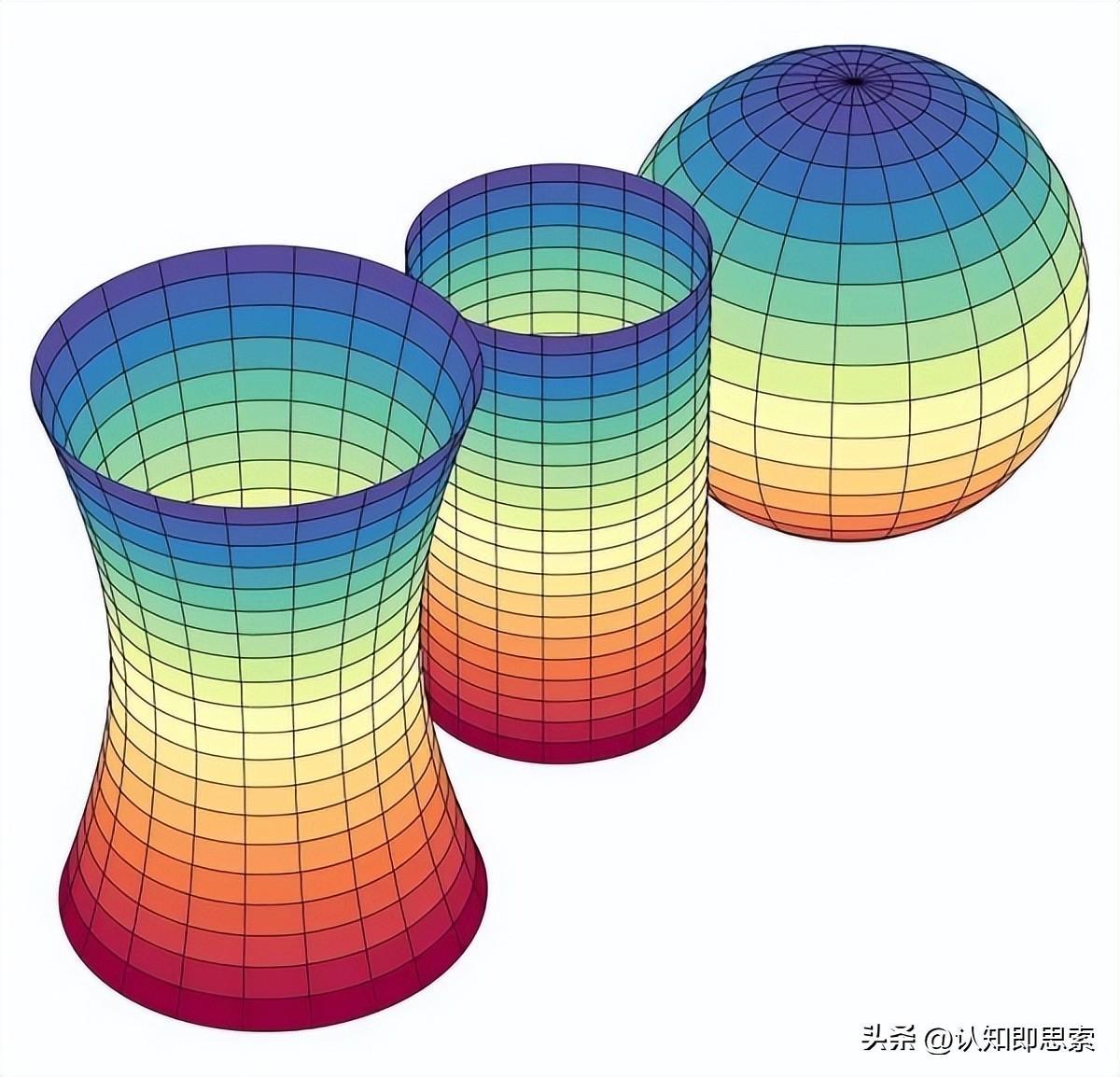
在线性代数中，研究的向量空间对元素的加法和数乘运算是封闭的。这意味着当我们对向量空间中的两个向量进行加法或数乘运算时，得到的结果仍然是该向量空间中的一个向量。此外，线性代数的基本概念和性质包括行列式、矩阵、行列式、逆矩阵、初等行变换等。这些基本概念和性质不仅有助于我们更好地理解线性代数的理论体系，而且对于解决实际问题也具有重要的指导意义：

你了解线性代数中的线性了吗？欢迎留言讨论~