平行四边形的面积公式大全（平行四边形，面积公式不用背，推导方法要清楚）

《平行四边形的面积》是人教版数学五年级上册第六单元《多边形的面积》里的第一节课。说起它的公式，大家一定觉得很简单，不就是“底×高”么？但是，这个公式是如何推导出来的，你还记得么？死记公式可以解决问题，但那不是学习数学的正确思路，学习数学的目的是培养孩子的抽象思维和推理能力，创新意识和实践能力。因此，一个公式是怎么得来的？它的推导过程很重要。

在学习“平行四边形的面积”之前，已经学过“长方形的面积”也知道长方形的面积=长×宽，因此，这节课我们可以结合长方形的面积来教学。

先从解决问题入手：学校大门前有两个花坛，一个长方形，一个平行四边形，这两个花坛哪一个大呢？要想回答“哪一个大”就得知道这两个花坛的面积。其中，长方形的面积是以前学过的内容，但平行四边形的面积不知道如何求，所以探究平行四边形面积的面积公式就是本节课的重点环节。

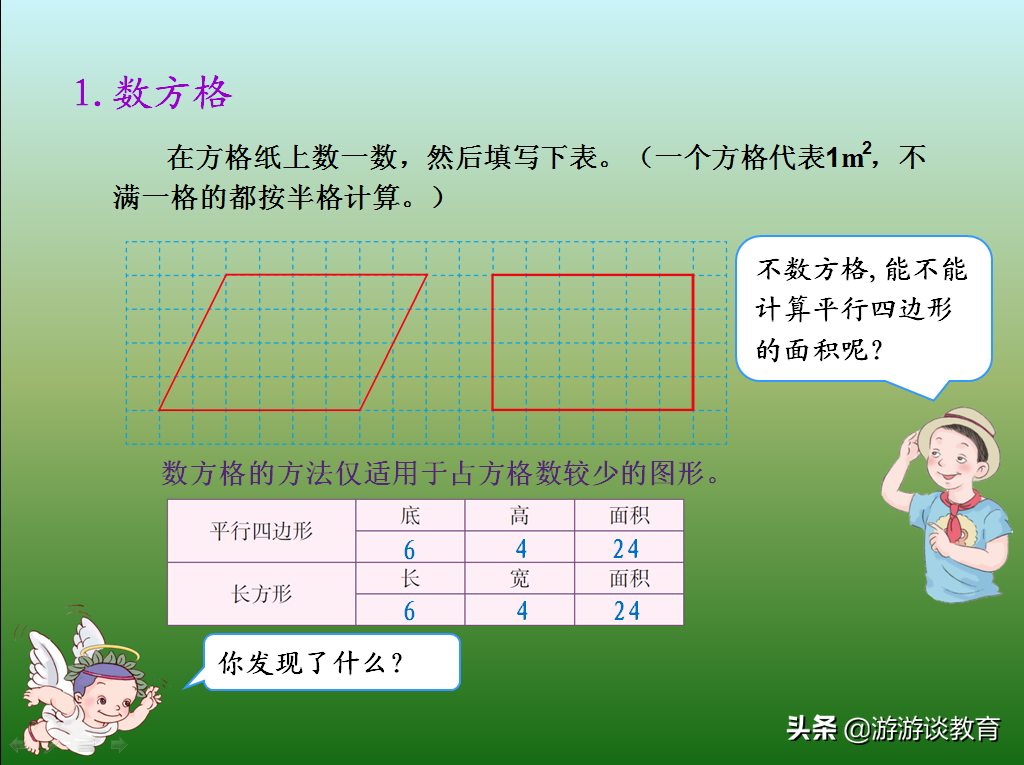
因为长方形的面积公式是用“数格子”的方法推导出来的，所以，平行四边形的面积也可以用“数格子”的方法试一试。通过数格子，可以发现不方便：一是平行四边形存在“半格”的情况，不好数；二是当图形占方格数较多的时候，更不好数；三是长方形可以通过“数方格”一下就推导出其面积公式是长×宽（几个几是多少用乘法），而平行四边形不是方方正正的形状，所以不明显。

因此，要想一想“不数方格，能不能计算平行四边形的面积呢？”这里，通过“数格子”完成了一个表格，可以从表格中发现，平行四边形和长方形是有联系的：底=高=6，高=宽=4，面积都等于24，找到这个突破口，我们就可以用“割补法”进行转化，看看能不能把平行四边形转化成长方形，它们之间是不是有底=高，高=宽的关系。

将平行四边形“割补”转化为长方形这里展示了3种情况：

（1）把平行四边形沿顶点到对边上的高切开，分成了一个直角△和直角梯形，然后把直角三角形平移到另一边，拼成一个长方形。从对比图上可以看出，长方形的长=平行四边形的底，宽=高，进行“割补”后，平行四边形的形状变了，但面积大小没有变，因此，长方形的面积=平行四边形的面积。

（2）把平行四边形从中间的高剪开，分成两个直角梯形，同样的把一边的图形平移到另一边，也可以拼成一个面积相等的长方形。

（3）把平行四边形分成两个小的锐角和中间一个大的六边形，分别平移两个小锐角，左边的移到右边，右边的移到左边，同样也能补成一个面积相等的长方形。

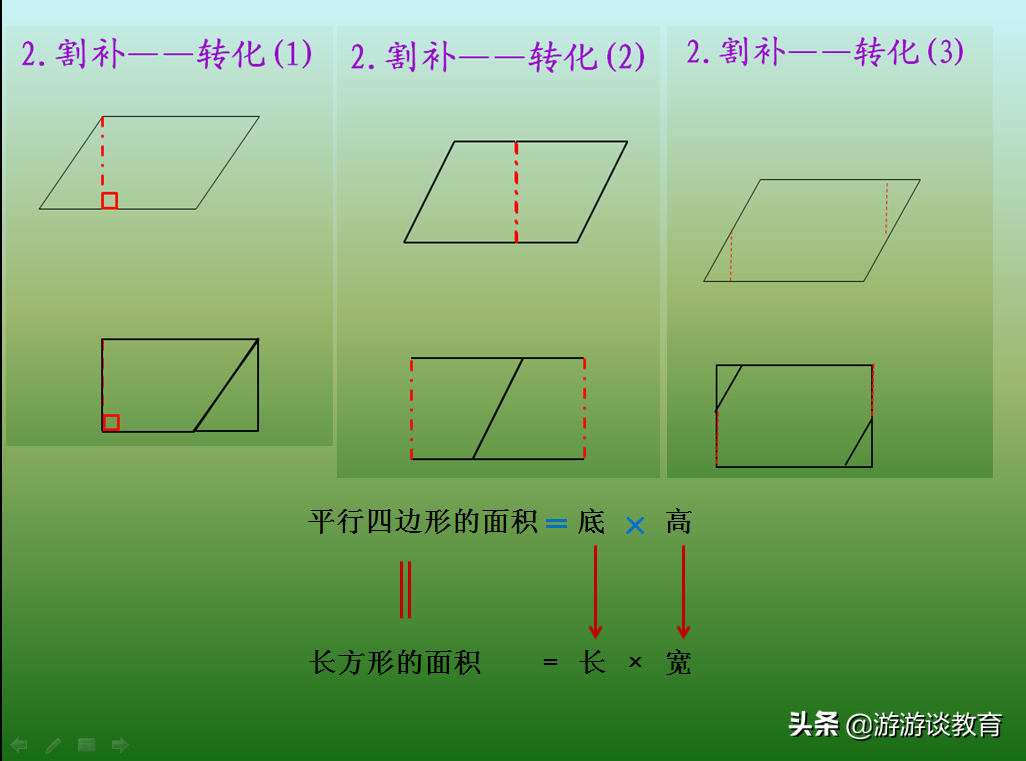
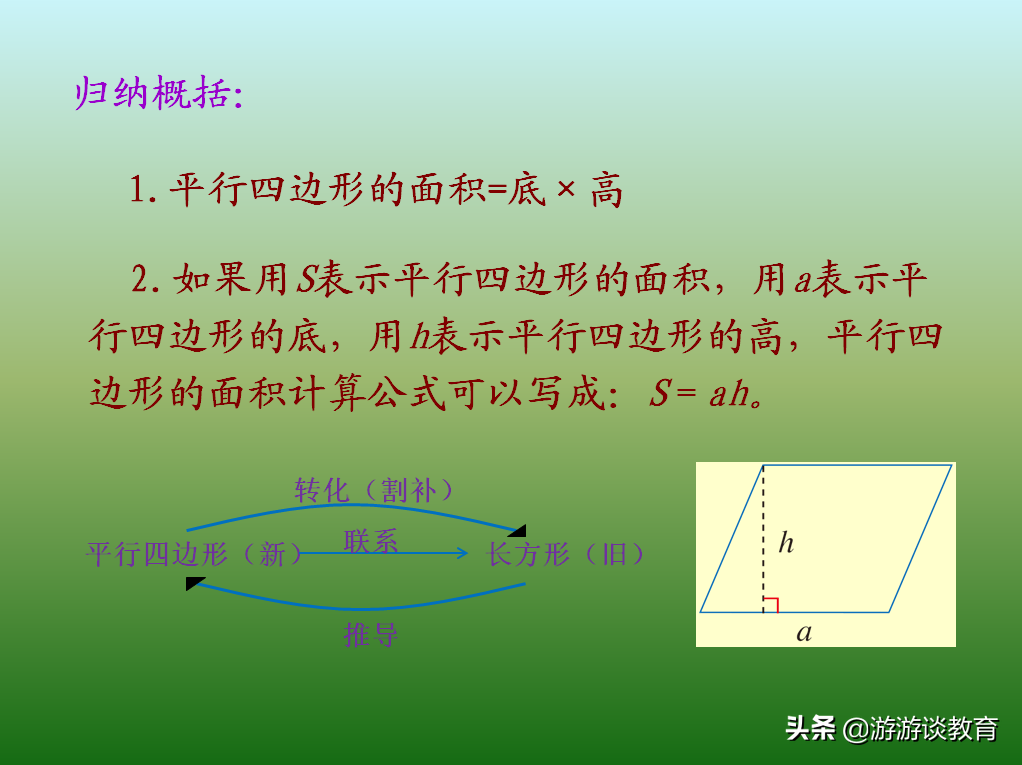
而在这三个转化过程中，我们都能从对比图中看出“长方形的面积=平行四边形的面积”、“长=底”、“宽=高”，因此，长方形的面积=长×宽，对应的平行四边形的面积就等于“底×高”了。

如果用S表示平行四边形的面积，用a表示平行四边形的底，用h表示平行四边形的高，平行四边形的面积计算公式可以写成：S＝ah。