直三棱柱的特点（正三棱柱和直三棱柱的特点）

球与其他几何体的切接问题，是近几年高考的热点，这种题目几乎在各省高考试题中都有涉及，主要考查空间想象能力和逻辑思维能力．

“切”“接”问题的处理规律

（１）“切”的处理

解决与球有关的内切问题主要是指球内切多面体与旋转体，解答时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．

（２）“接”的处理

把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．

下面就近几年高考题对球与其他几何体的切接作深入的探究，从而使学生掌握高考命题的趋势和高考的出题思路．

１．由球的定义确定球心

若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球．也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体外接球的球心．

①长方体或正方体的外接球的球心是其体对角线的中点；

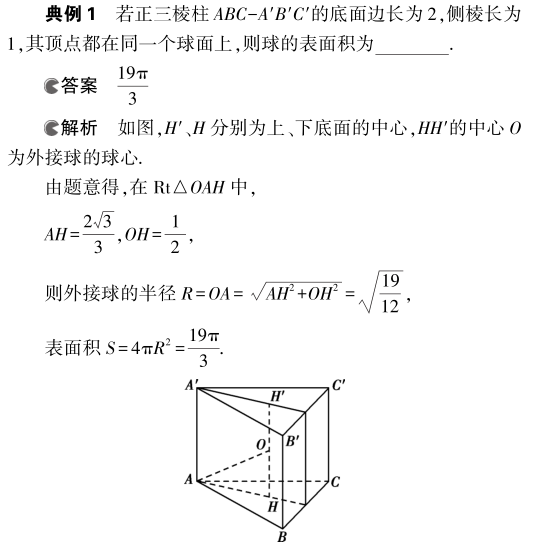
②正三棱柱的外接球的球心是上、下底面中心连线的中点；

③直三棱柱的外接球的球心是上、下底面三角形外心连线的中点；

④正棱锥的外接球的球心在其高上，具体位置可通过建立直角三角形运用勾股定理计算得到；

⑤若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心．

２．构造长方体或正方体确定球心

①正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补成长方体或正方体；

②同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补成长方体或正方体；

③若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体；

④若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体.

３．由球的性质确定球心

本题运用公式 Ｒ ^２＝ｒ^２＋ｄ^２ （ｒ 为三棱锥底面外接圆的半径，Ｒ 为三棱锥外接球的半径，ｄ 为球心到三棱锥底面中心的距离）求球的半径，该公式是求球的半径的常用公式．本题的思路是探求正棱锥外接球半径的通法，该方法的实质是通过寻找外接球的一个轴截面，把立体几何问题转化为平面几何问题来研究．